Bellman Equation

The page consists of two sections.

• Bellman Equation Basics
• Bellman Equation Advanced

Bellman Equation Basics

An introduction to the Bellman Equations for Reinforcement Learning

Important Bellman Concepts

• STATE: a numeric representation of what the agent is observing at a particular point of time in the environment. (e.g., raw pixels on the screen)
• ACTION: the input the agent provides to the environment, which is calculated by applying a policy to the current state. (e.g., control buttons pressed, joystick)
• REWARD: a feedback signal from the environment reflecting how well the agent is performing the goals of the game. (e.g., coins collected, enemies killed)

Goal of Reinforcement Learning

Given the current state we are in, choose the optimal action which will maximize the long-term expected reward provided by the environment.

What Question Does the Bellman Equation Answer?

Given the state I'm in, assuming I take the best possible action now and each subsequent step, what long-term reward can I expect?

What is the VALUE of the STATE?

info

It helps us evaluate the expected reward relative to the advantage or disadvantage of each state.

Bellman Equation

For deterministic environments.

$$V(s) = \max_a(R(s,a) + \gamma V(s\prime))$$

• $s$ a given state.
• $V(s)$ the VALUE of a given state.
• $\max_a$ means that all the actions available in the state we are in, we pick the action which is going to maximize the value.
• $R(s, a)$ is the reward of the optimal action in state $s$.
• $\gamma$ is the discount factor.
• $s\prime$ is the state after performing the action $a$.

info

At each step, we need to know what the optimal action is.

tip

Gamma $\gamma$

• Successful values range between 0.9 and 0.99.
• A lower value encourages short-term thinking.
• A higher value emphasizes long-term rewards.

Example

At $V=1$, $R(s,a)=1$ means we can get a reward of 1 if we take the action in state because it can get us to the green cell. $V(s\prime)=0$ because $s\prime$ is the terminal state and there is no value associated with it.

Bellman Equation Advanced

For stochastic environment.

Bellman Equation Advanced for Reinforcement Learning

Markov Decision Process

State -> Action

We're in a state we choose an action, and now there are several possible $s\prime$ states we could end up being in based on random probability.

Each possible state transition from an action has an exact probability and all the probabilities add up to 1.

info

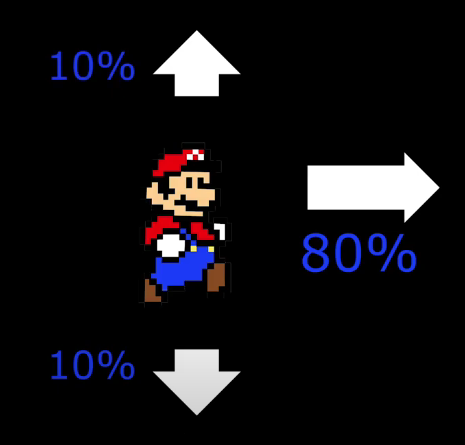
The probability of future transitions only depends on the present and the past doesn't matter.

New Bellman Equation

For stochastic environment.

1. Loop through every possible state that we can transition to after taking a specific action.
2. Multiply the VALUE of that state by its probability of occurring.
3. Sum them all together.

$$V(s) = \max_a(R(s,a) + \gamma \sum_{s\prime} {P(s,a,s\prime) V(s\prime)})$$

$\sum_{s\prime}$ means that we are looping all the $s\prime$ that the optimal action could possibly lead us to.