Australia Map Coloring

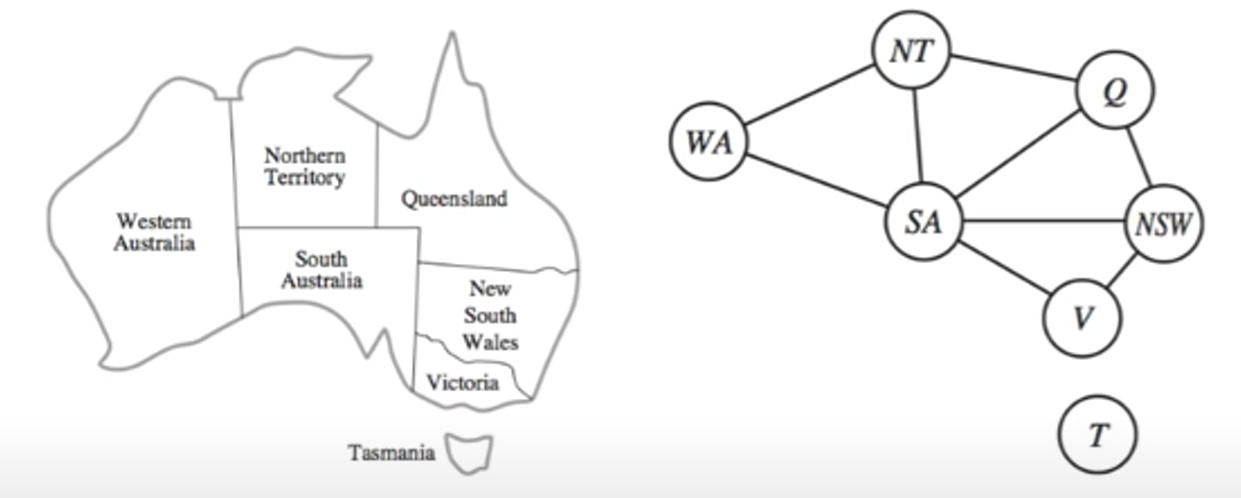
• Color each region using either red, green, or blue.
• No adjacent region can have the same color.

Formulate the Problem X, D, C

According to the definition of CSP. We can define variables to be the regions:

$$\chi= \{SA, NSW, NT, Q, WA,V ,T\}$$

The domain of each variable is the set $D=\{red,green,blue\}$.

The constraints require neighboring regions to have distinct colors. There are 9 constraints:

$$C = \{ SA \not = WA, SA \not = NT, SA \not = Q, SA \not = NSW, SA \not = V, \\ WA \not = NT, NT \not = Q, Q \not = NSW, NSW \not = V \}$$

Here we are using abbreviations; $SA \not = WA$ is a shortcut for <(SA,WA), $SA \not = WA$>, where $SA \not = WA$ can be fully enumerated as

$$\{(red,green), (red, blue), (green, red), (green, blue), (blue,red), (blue, green) \}$$

Constraint Graph

The CSP can be visualized as a constraint graph, as shown at the beginning of this page.

• The nodes of the graph correspond to variables of the problem.
• An edge connects any two variables that participate in a constraint.