Skip to main content

Gaussian Mixture Models (GMMs)

GMM extends k-means, such that rather than having hard cluster boundary, we now have a set of distributions, and we can capture uncertainty. For example, we'll be able to tell when a point is close to being part of two different classes.

  • A GMM will attempt to fit a set of Gaussian distributions to the data, and each Gaussian will capture one cluster (or component) of the data.
  • GMMs build upon K-means, using K-means for initialization before using Expectation Maximization to fit the model.
info

Unlike K-means, GMMs can capture different shaped clusters, and clusters can overlap.

It can also measure how much a point belongs to multiple cluster centres and how likely a point is to arise from the distribution. This has excellent applications for outlier/anomaly detection.

Advantages​

  • Soft decisions
  • Likelihood

The big advantage of a GMM over k-means is that we get the soft decisions. K-means will assign a point to a cluster, and won't give any indication if there were multiple centres that could have fit that cluster.

Secondly, a GMM will give us the likelihood of a point for each Gaussian, so we get a better idea of where the point lies, and how close it is to multiple cluster centres.

info

In machine learning, we want to avoid hard decisions for as long as possible.

K-means and it's assignment of points to a cluster can be seen as a hard decision. After we assign a point to a cluster, we lose any other information about where that point lies.

A GMM helps overcome this. Now we can do a soft assignment, and help carry forward the uncertainty about which cluster a point belongs to until we get further into our analysis.

Python​

from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=2)
gmm.fit(X)

We can get:

  • the means of the components, i.e. the centers of each cluster.
  • the weights of the components, i.e. the relative size of each cluster.
  • the covariances of each cluster, this gives us the shape of the clusters.
print(gmm.means_)
print(gmm.weights_)
print(gmm.covariances_)

When assign points to clusters, we don't make a hard decision. Rather we get the likelihood of the point arising from each component.

print(gmm.predict_proba([[0.3,0.3]]))
print(gmm.predict_proba([[2.0,2.0]]))
# below indicates that the first point belongs to the second class,
# the second point belongs to the first class
[[0.0064498 0.9935502]]
[[0.99719157 0.00280843]]

We can visualize this soft decision.

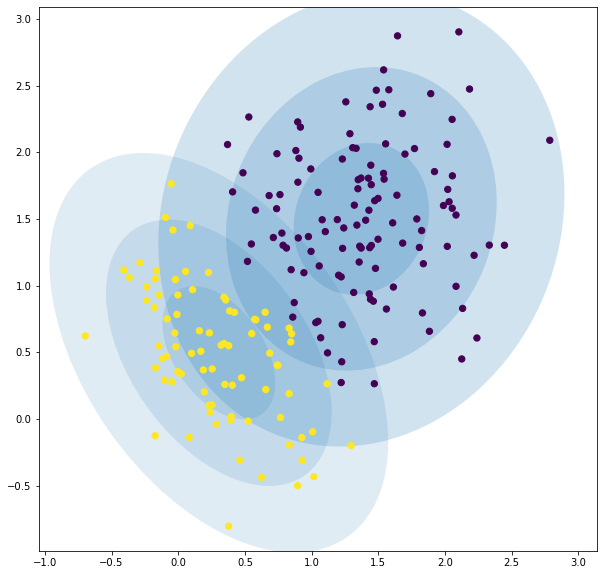
gmm visualization

What we see here is that the two components overlap, so we have regions that points can belong to both clusters.

References​