Skip to main content

Regularization

Regularization is a strategy used to build better-performing models by reducing the odds of overfitting, or when your model does such a good job of matching your training data that it performs badly on new data. In other words, regularization is a way to help your model generalize better by preventing it from becoming too complex.

Reduce the magnitude and/or the number of parameters to reduce model complexity.

One way to regularize a linear regression is to add a constraint to the loss function:

∑i=1nϵ2+λP\sum^n_{i = 1} {\epsilon^2 + \lambda P }

λ\lambda is a hyperparameter that controls the influence of our penalty.

info

Regularization seeks to penalize complex models

  • A small change in input should lead to a small change in output value.
  • Model complexity often leads to overfitting.

There are three main types of constraints: Ridge (L2), Lasso (L1), and Elastic Net.

Ridge Regression (L2)​

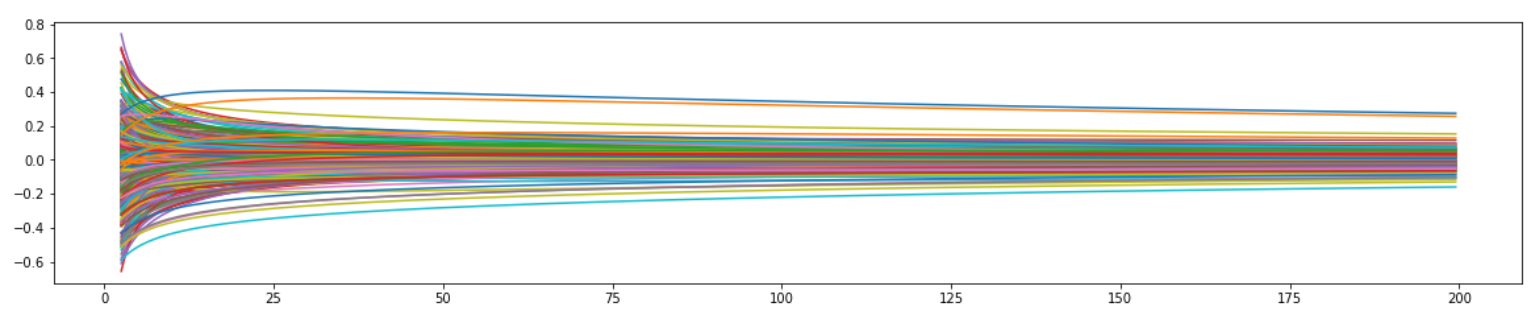
Ridge regression is also called L2 regularization. It adds a constraint that is the sum of the squared coefficients.

∑i=1M(yi−∑j=1Pwj×xij)2+λ∑j=1P∣∣wj∣∣2\sum^{M}_{i = 1} {\left( y_i - \sum^P_{j = 1} {w_j \times x_{ij}} \right)^2} + \lambda\sum^P_{j = 1} {||w_j||_2}

The second term is also known as shrinkage penalty.

  • λ=0\lambda = 0, this penalty term has no effect and ridge regression produces the same coefficients as least squares.
  • As λ→∞\lambda \to \infty, the shrinkage penalty becomes more influential, the coefficients will approach 0.

Trace Plot​

ridge-trace-plot

Python​

Use sklearn's Ridge Regression.

from sklearn.linear_model import Ridge
import numpy as np
n_samples, n_features = 10, 5
rng = np.random.RandomState(0)
y = rng.randn(n_samples)
X = rng.randn(n_samples, n_features)
clf = Ridge(alpha=100.0) # alpha controls the strength of the penalty
clf.fit(X, y)

Lasso Regression (L1)​

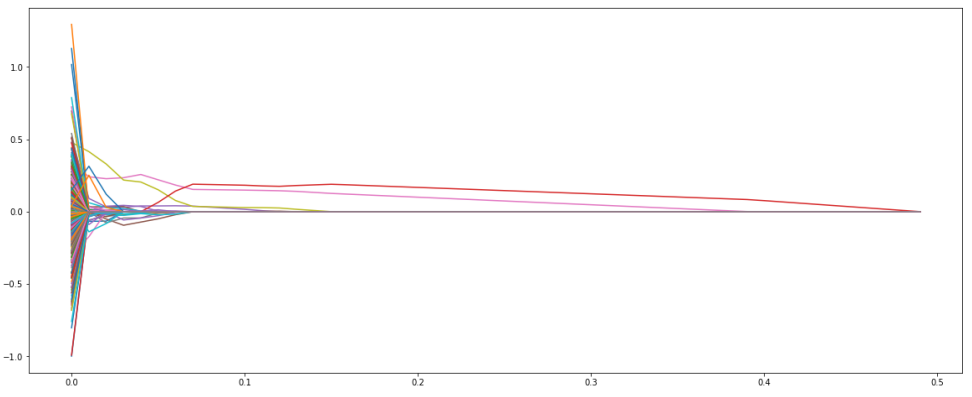
Lasso regression is also called L1 regularization. It also adds a constraint that is the sum of absolute coefficients.

∑i=1M(yi−∑j=1Pwj×xij)2+λ∑j=1P∣∣wj∣∣1\sum^{M}_{i = 1} {\left( y_i - \sum^P_{j = 1} {w_j \times x_{ij}} \right)^2} + \lambda\sum^P_{j = 1} {||w_j||_1}

It forces some of the coefficients to be zero and results a simpler model. Therefore it can be used to perform feature selection.

Trace Plot​

lasso trace plot

Python​

Use sklearn's Lasso Regression.

from sklearn.linear_model import Lasso
clf = Lasso(alpha=0.1) # alpha controls the strength of the penalty
clf.fit(X = [
                [0, 0],
                [1, 1],
                [2, 2]
            ],

        y = [0, 1, 2])

print(clf.coef_)

print(clf.intercept_)

Elastic Net​

Elastic Net is the combination of the L1 regularization and L2 regularization. It can both shrink the coefficients as well as eliminate some of the insignificant coefficients.

Standardization​

The values are transformed so their mean is 0, and their standard deviation is 1.

x=x−μσx = \frac{x - \mu}{\sigma} 
def standardize(data):
  """ Standardize/Normalize data to have zero mean and unit variance

  Args:
    data (np.array):
      data we want to standardize

    Returns:
      Standardized data, mean of data, standard deviation of data
  """
  mu = np.mean(data, axis=0) # rows - top to bottom
  sigma = np.std(data, axis=0) # rows - top to bottom
  scaled = (data - mu) / sigma
  return scaled, mu, sigma
info

Why standardization?

  1. For a given dataset, dimensions are usually in different scales. With regularization penalty, some dimensions might be penalized heavier than other dimensions.
  2. Easier to visualize.

References​