Data Representation

Computer can only store bits. In order to display text or other forms of data, we need a way to use bits to represent them aka "representing data as bits".

Text as Bits

Character data is comprised of symbols and numerals that are not used in calculations. And it is commonly referred to as "text".

Examples:

• Symbols (e.g., Latin letters, chinese characters...)
• Numerals (0,1,2,3,...9)
• Unprintable characters (space, newline, tab)

Encoding

To represent characters as bit strings we need an encoding.

Character encoding is the process of assigning numbers to graphical characters, especially the written characters of human language, allowing them to be stored, transmitted, and transformed using digital computers.

Requirements:

• A set of characters to be represented.
• A length n for bit strings. (e.g., 7-bit ASCII char)
• A mapping from characters to bit strings (one-to-one relationship).

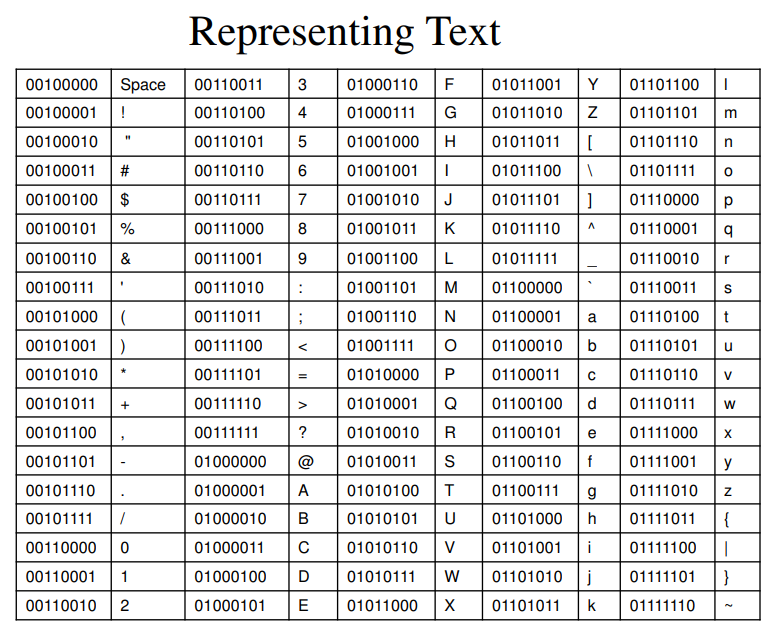
ASCII

ASCII abbreviated from American Standard Code for Information Interchange, is a character encoding standard for electronic communication. It was designed for teleprinters.

• Letters are ordered lexicographically.
• Numbers 0-9 are ordered lexicographically.
• Related characters are organized in blocks (upper case, lower case, and numbers).
• Upper case vs. lower case is just 1 bit.
• Requires 7 bits for each character. The leftmost bit is set to 0.
• Provides 128 characters ($2^7$).

ASCII Chart:

ASCII Chart

Encode "the" in ASCII:

character	ASCII Code
t	$0\ 111\ 0100$
h	$0\ 110\ 1000$
e	$0\ 110\ 0101$

info

bit 1 is at the rightmost column.

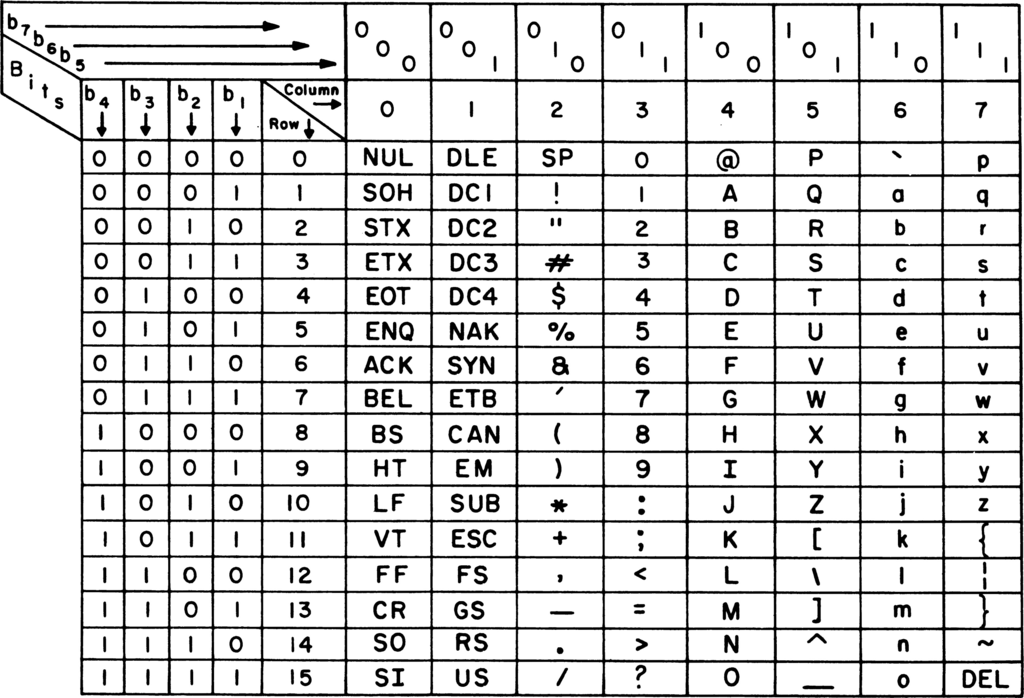
Unicode

👍 Unicode is a modern system of character encoding that supports most writing systems.

• UTF-32 uses 32 bits for each character.
• UTF-16 uses one or two 16-bit strings per code point.
• UTF-8 ues between one and four 8-bit strings per code point. It is backwards compatible with 7-bit ASCII.

info

Use "🪟+ ." to type emoji.

Numbers as Bits

How to store numbers as bits? We can use binary numbers. Consider the following example.

note

Example: $1010$

Starting from position 0 (rightmost)

• 0 has a multiplier of $2^0 = 1$
• 1 has a multiplier of $2^1 = 2$
• 0 has a multiplier of $2^2 = 4$
• 1 has a multiplier of $2^3 = 8$
• Total is 10 (in base-10).

Adding Binary Numbers

We can use bit operations to build half adders and full adders to perform additions.

binary math operations - half/full adder

Half Adder

A half adder can be used to add two 1-bit numbers.

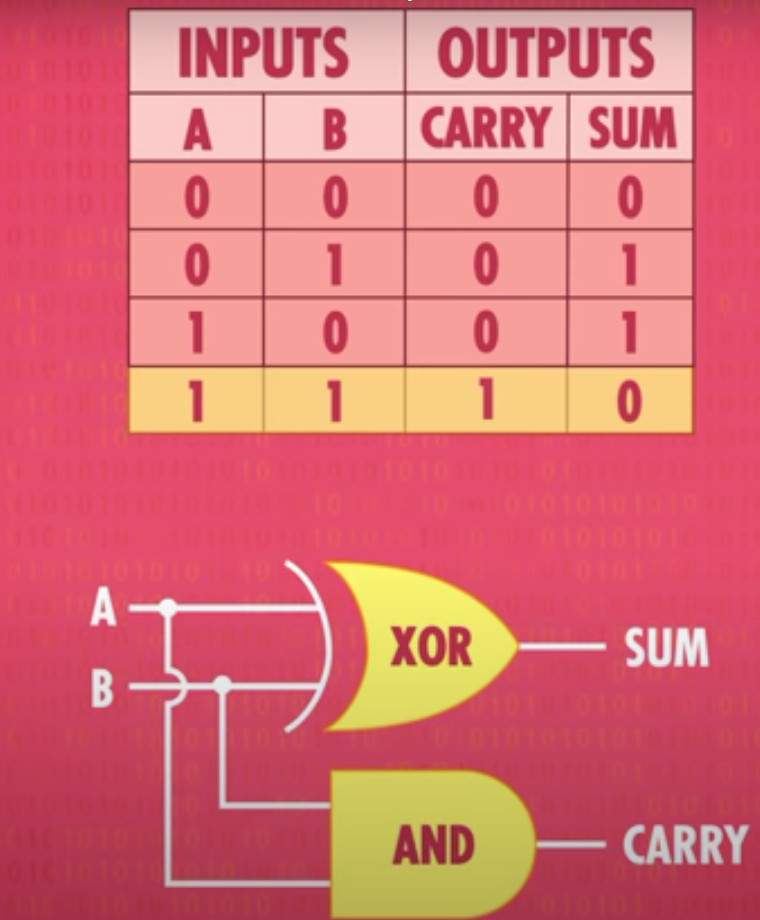
Suppose we have 1-bit binary numbers $\bar{x}$ and $\bar{y}$. We want to compute the result $\bar{x} + \bar{y} = \bar{z}$.

$$\begin{aligned} \bar{z}_0 & = \bar{x}_0 \oplus \bar{y}_0 \\ \bar{z}_1 & = \bar{x}_1 \& \bar{y}_1 \end{aligned}$$

Full Adder

The half adder is used to add only two numbers. To overcome this problem, the full adder was developed. The full adder is used to add three 1-bit binary numbers A, B, and carry C. The full adder has three input states and two output states i.e., sum and carry.

-- javatpoint.com

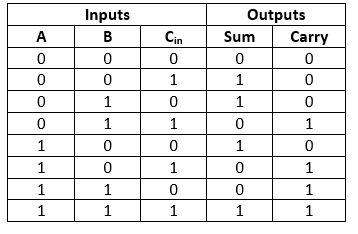
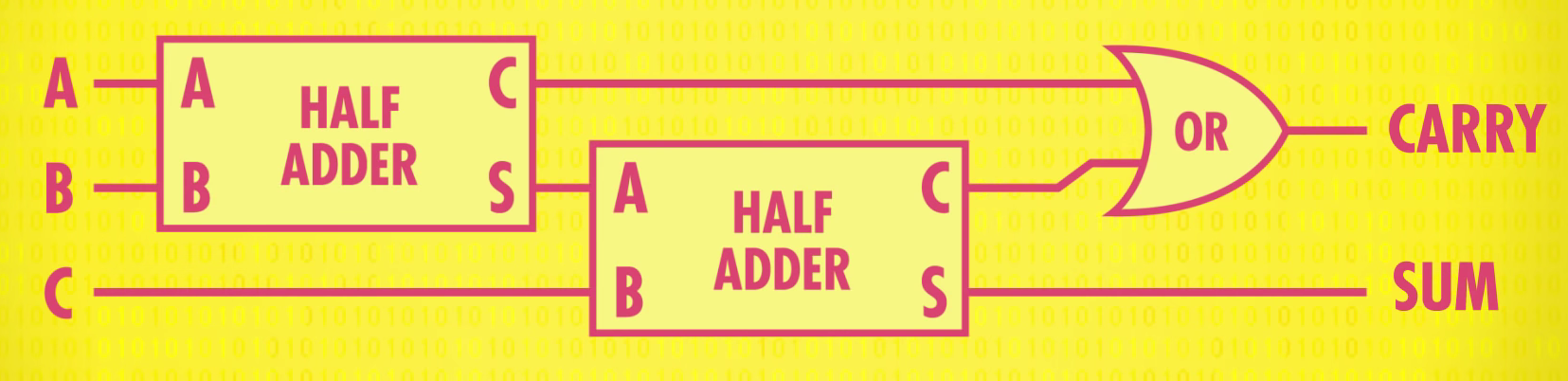
In general, for n-bit binary numbers $\bar{x}$ and $\bar{y}$. The sum $\bar{z}$ is a n+1-bit binary numbers where

$$\begin{aligned} \bar{z}_j & = \bar{x}_j \oplus \bar{y}_j \oplus \bar{c}_j \\ \bar{c}_{j+1} & = (\bar{x}_j \& \bar{y}_j) | (\bar{x}_j \& \bar{c}_j) | (\bar{y}_j \& \bar{c}_j) \end{aligned}$$

Modular Arithmetic

What happen when we have a number that is too big? (e.g., exceeds 8-bit limit)

Answer: CPU will perform integer modulo $2^n$ where $n$ is the number of bits.

EXAMPLE

Suppose we are adding two 8-bit numbers.

10000000(128) + 10000001(129) = 100000001(257, 9-bits)

Drop the leftmost bit to get 8-bits 00000001(1).

This "dorp" action can be achieved by performing a mod $2^n$ on the result. $n$ is the number of bits.

$$257 \ \textrm{mod} \ 256 = 1$$

2's Complement

2's complement is a method of signed number representation.

Properties of 2's complement:

• For $n$ bits, we can represent from $-2^{n-1}$ to $2^{n-1} -1$
  • e.g., 8-bit strings, the range is $-128$~$127$
• If the leftmost bit is 0, then the number is positive. Otherwise, it is negative.
• Always perform $\textrm{mod}\ 2^n$ after each addition.

3-bit 2's complement table:

Bits	Unsigned value	Two's complement value
000	0	0
001	1	1
010	2	2
011	3	3
100	4	-4
101	5	-3
110	6	-2
111	7	-1

Hexadecimal

Hexadecimal is a base-16 number system. So the numeral in position $i$ gets multiplier of $16^i$.

Base-10, Base-2, and Base-16 table:

Decimal (Base 10)	Binary (Base 2)	Hexadecimal (Base 16)
0	0011	0x0
1	0001	0x1
2	0010	0x2
3	0011	0x3
4	0100	0x4
5	0101	0x5
6	0110	0x6
7	0111	0x7
8	1000	0x8
9	1001	0x9
10	1010	0xA
11	1011	0xB
12	1100	0xC
13	1101	0xD
14	1110	0xE
15	1111	0xF

Interpret Hex

Hex to base-2 string, just need to concatenate the converted strings together.

BASE-2

Write 4F as an 8-bit string:

4 -> 0100, F -> 1111. So 4F -> 0100 1111

Hex to base-10 number, the steps are similar to "convert base-2 to base-10"; the multiplier.

BASE-10

Write 4F as a base-10 number:

4 gets a multiplier of $16^1$ because it is in position 1. F(15) gets a multiplier of $16^0$ because it is in position 0.

$4 \times 16^1 + 15 \times 16^0 = 79$

Python

How to format integer in hex?

>>> f"{79:X}"
'4F'
>>> f"{255:X}"
'FF'

Floating Point Numbers

A floating-point number is represented approximately with a fixed number of significant digits (the significand) and scaled using an exponent in some fixed base; the base for the scaling is normally two.

-- wikipedia

References

• Lecture Notes
• Computer Science Crash Course
• Week2 Resources
• Full Adder