Graphs

A graph is an irreflexive and symmetric relation.

• A graph $G$ is a pair $(V,E)$
• The set $V$ is the vertices or nodes of $G$
• The set $E \subseteq V \times V$ is the edges of $G$
• For every $(u,v) \in E$ we have $(v,u) \in E$ - symmetric
• There are no edges $(v,v)$ - irreflexive

This type of graph is called loop-free undirected graph, referring to irreflexive and symmetric.

Graph Visualization

We usually visualize graphs as a set of points (vertices) connected by line (edges).

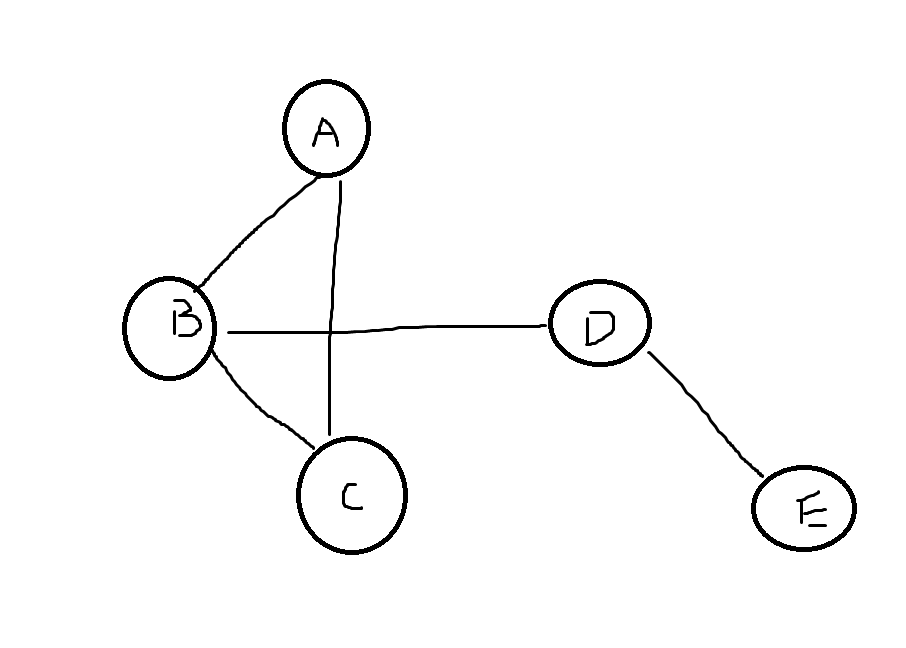
Graph Definitions

Neighbors

If $(u,v) \in E$ then we say $u$ and $v$ are adjacent. We also say that $u$ and $v$ are neighbors.

tip

If there is an edge between two vertices then they are adjacent.

The neighborhood of a vertex $u$ is the set of $u's$ neighbors.

$$N_G(u) = \{v \in V: (u,v) \in E\}$$

The neighborhood of a set of vertices $S \subseteq V$ is a set that contains all neighbors of vertices in $S$.

$$N_G(S) = \{v \in V: (u,v) \in E \land u \in S \}$$

def N(G, u):
    """
    Get the neighbors of a vertex.
    G: a graph (V, E)
    u: a vertex
    """
    V, E = G
    return {v for v in V if (u, v) in E}

def NS(G, S):
    """
    Get the neighbors of a set of vertices.
    G: a graph (V, E)
    S: a set of vertices
    """
    neighbors = set()
    for u in S:
        neighbors = neighbors.union(N(G, u))
    return neighbors

def NS_2(G, S):
    V, E = G
    return {v for v in V for u in S if (u,v) in E}
# the graph from the visualization section
V = {"A", "B", "C", "D", "E"}
E = { 
    ("A","B"),("B","A"),
    ("A","C"),("C","A"),
    ("B","C"),("C","B"),
    ("B","D"),("D","B"),
    ("D","E"),("E","D") 
    }
G = (V, E)

print("Vertices:", V)
print("Edges:", E)
print("Neighbors of A:", N(G, "A"))
print("Neighbors of {A, D}:", NS(G, {"A","D"}))

"""
Vertices: {'D', 'C', 'E', 'A', 'B'}
Edges: {('C', 'B'), ('E', 'D'), ('C', 'A'), ('D', 'E'), ('B', 'A'), ('B', 'C'), ('D', 'B'), ('B', 'D'), ('A', 'C'), ('A', 'B')}
Neighbors of A: {'B', 'C'}
Neighbors of {A, D}: {'B', 'C', 'E'}
"""

Degrees

The degree of a vertex $u$ is the size of its neighbors.

$$d(u) = |N_G(u)|$$

info

Every edge $(u,v)$ adds 1 to the degree of $u$ and the degree of $v$, so we have the sum of degrees:

$$2|E| = \sum_{u \in V} d(u)$$

note

We count $(u,v)$ and $(v,u)$ together as a single edge.

Incident

If $e=(u,v) \in E$, we say $e$ is incident with u (and v).

Graph Examples

• The set of computers in a network, where $u$ and $v$ are adjacent if they are connected physically (Ethernet, wifi).
• The set of cities in the world, $u$ and $v$ are adjacent if there is a direct flight.

Handshaking Lemma

Since the sum of degrees is even, there must be an even number of vertices with odd degree.

References

• QUT Materials