Graph Connectivity

Path

A path is a sequences of vertices $[v_1, v_2, v_3,\dots, v_j]$ such that:

• No vertex appears more than once.
• $v_k$ is adjacent to $v_{k+1}$. for each $k = 1 \dots j-1$.
• The length of the path is $j-1$ which is the number of edges.

Example

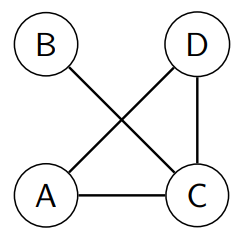
• $A,D,C,B$ is a path of length 3.
• $A,C$ is a path of length 1.
• $D,C,A$ is a path of length 2.

Cycle

A cycle is just like a path, but $v_1 = v_j$, so that it loops back on itself.

• The length of a cycle is $j-1$, which is the number of edges, and also the number of vertices.
• We don't care about the starting vertex of a cycle. So $A,B,C,A$ is the same cycle as $B,C,A,B$.
• We might not use the above notation (duplicate the start/end vertex) to represent a cycle. Instead we will use "cycle $A,B,C$". Note: this is different from path, path can be represented by "path $A,B,C$".

Example

• $A,D,C,A$ is a cycle of length 3.

Connectedness

If there is a path from $u$ to $v$ for every $u,v \in V$, then we say that $G$ is connected. Otherwise, we say $G$ is disconnected.

Example

The graph is connected.

Connected Component

If for every $u,v \in S \subseteq V$ there is a path between $u$ and $v$, and there are no paths to any vertices outside $S$.

Then we call $S$ is a connected component of $G$.

Example

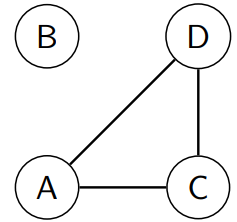
The graph is disconnected.

The connected components are $\{B\}$ and $\{A,C,D\}$

Distance

The distance between vertices $u$ and $v$ is the length of a shortest path from $u$ to $v$.

Calculating Distances

Given a fixed vertex $u$, we define:

• $D_j$ to be the set of vertices that is $j$ distance from $u$. (explored)
• $V_j$ to contain the set of vertices that has distance at least $j$ from $u$. (unexplored)

$$V_j= \begin{cases} V & :j=0 \\ V_{j-1} \setminus D_{j-1} & :j>0 \end{cases}$$

$$D_j= \begin{cases} \{u\} & :j=0 \\ N_G(V_j, D_{j-1}) & :j>0 \end{cases}$$

The visualization of the graph can be found here.

_assets-07/distance_classes.py

def distance_classes(V:set, E:set, u):
    """
    V: a set of vertices.
    E: a set of edges.
    u: the starting vertex.

    return: A list D. The vertices in D[1] is 1 distance from u.
    """
    D = [{u}]
    V_unexplored = V - {u}

    return distance_classesR(V_unexplored, E, D)

def distance_classesR(V,E, D):
    V_unexplored = V - D[-1]
    if len(V_unexplored) == 0:
        return D
    D_new = NS(V_unexplored, E, D[-1])
    D = D + [D_new]
    return distance_classesR(V_unexplored, E, D)

def NS(V,E,S):
    return {v for u in S for v in V if (u,v) in E}

V = {"A", "B", "C", "D", "E"}
E = { 
    ("A","B"),("B","A"),
    ("A","C"),("C","A"),
    ("B","C"),("C","B"),
    ("B","D"),("D","B"),
    ("D","E"),("E","D") 
    }
print(distance_classes(V,E, "A"))
# [{'A'}, {'C', 'B'}, {'D'}, {'E'}]

Bipartite Graph

If we are able to separate/partition vertices into two sets $(A,B)$ such that vertices within each set are not adjacent, then we call $(A,B)$ a bipartition of $G$.

Theorem

A graph $G$ is bipartite iff $G$ has no cycles of odd length.

What is a Bipartite Graph? | Graph Theory

Vocabulary

Cannot find definitions for "bipartite".

References

• QUT Materials