Trees

A connected graph without any cycles is called a tree.

• A tree always has $|V| - 1$ edges.
• There is always a unique path between any two vertices in a tree.

A graph (not necessarily connected) without any cycles is called a forest. In such graph, each connected graph is a tree.

Rooted Trees

In a tree we can specify a special vertex, called the root. Any vertex can be the root.

Example

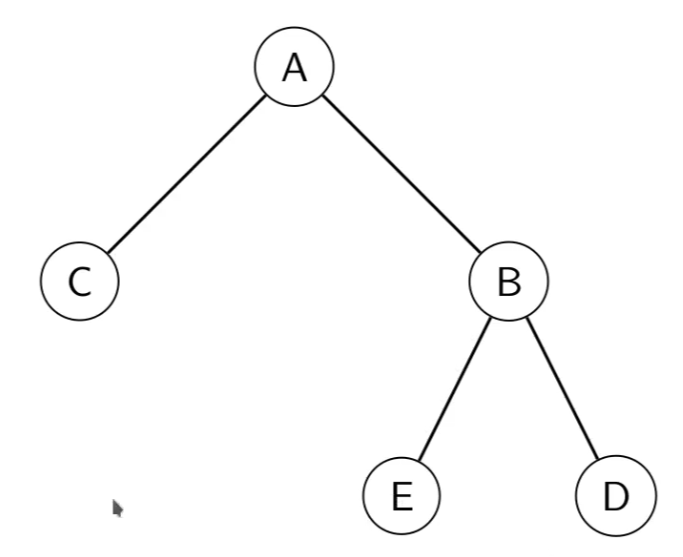
The root is chosen to be $A$.

• $B's$ ancestors is just $A$.
• $D's$ ancestors are $B$ and $A$.
• $A's$ children are $C$ and $B$.
• $B's$ descendants are $E$ and $D$.
• The leaves are $C$, $E$, and $D$.

Parent

The parent of a vertex is the first vertex in the unique path to the root.

We call the parent of v, $P(v)$

info

The root has no parent.

Ancestors

The ancestors of a vertex are its parent and its parent's parent, etc. All the way to the root.

We call the set of ancestors of a vertex v, $A(v)$.

• If v is the root, then $A(v)=\empty$
• If v is not the root, then $A(v)=\{P(v)\} \cup A(P(v))$

Children

The children of a vertex are all its neighbors except its parent.

Descendants

The descendants of a vertex is all its children, all its children's children, etc.

We call the set of children of a vertex v, $C(v)$ and the set of descendants $D(v)$.

• If the vertex is the root then $C(v)=N_G(v)$, otherwise $C(v)=N_G(v) \setminus P(v)$
• The descendants are given by:
  $$D(v) = C(v) \cup_{u \in C(v)} D(u)$$

info

Why is there no base case?

It exists, it just built in to the notation. If $C(v)=\empty$ then the big union will disappear.

Leaf

A vertex without children is called a leaf.

Subgraph

Induced Subgraph

Subtree

Spanning Tree

Use Cases

• In networking, we often identiy a spanning tree of the network and only send packets along the edge of the spanning tree. This prevents packets from going around the network in a cycle.
• The graph of the shortest paths from a vertex will form a rooted spanning tree.

Vocabulary

intrinsic

noun

1. A built-in function that is implemented directly by the compiler, without any intermediate call to a library.
2. An ability possessed by a character and not requiring any external equipment.

adjective

1. Innate, inherent, inseparable from the thing itself, essential.
2. (of a body part) Situated, produced, secreted in, or coming from inside an organ, tissue, muscle or member.

descendants

noun

1. One who is the progeny of a specified person, at any distance of time or through any number of generations.
2. A thing that derives directly from a given precursor or source.
3. A later evolutionary type.
4. A language that is descended from another.
5. A word or form in one language that is descended from a counterpart in an ancestor language.